月までの距離は何km？

では、本題に入る前に頭の準備運動。

月食の説明図をみてください。

まず、 地球の影が細くなって消えてしまう点 P は、地球から何 km 離れた所か求めてみましょう。

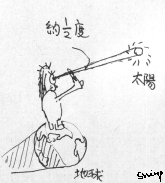
5円玉を手にもって腕をのばしたとき、5円玉の穴にちょうど 太陽が入ります。つまり、太陽の見ための大きさは、約54cm 先 にある直径5mm の円の大きさとおなじくらいです。

上の図を見てくださいね。 太陽の見ための大きさを角度で表すと約 2分の1 度です。

月食の説明図（上図）とみくらべてください。

地球の影がなくなるP点が右の図では目の位置に対応し、 地球が5円玉の穴に対応すると思うと、点Pの頂角が、 約 2分の1 度であることがわかります。

このことから、地球の直径がわかっているので、 地球から P までの距離が約140万km である事が 計算できます。（数学の得意な人は計算してみてください)

月も太陽のように5円玉の穴の中にちょうどはいります。

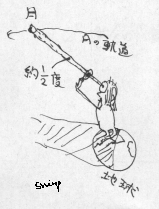
月のみための大きさは、太陽とほとんど同じ、約 2分の1 度です。

日食の時に太陽が月によってちょうどかくされることは、太陽も月もほとんどみかけの大きさが 同じである事を示しています。 しかし、 なぜ見ための大きさが太陽も月も同じなのか？といわれても、偶然としか言いようがありません。

見ための大きさがわかっても、月までの距離と月の実際の大きさはわかりません。 54cm さきの5mmの円も、 5.4mさきの5cmの円も、 5万4千kmさきの500kmの円も 見ための大きさはみんな同じで区別つきません。

月までの距離はわかりませんが、目の位置（地球）を 頂点Q として 頂角が約 2分の1 度、で月の直径を底辺とする2等辺三角形ができます。

以上で準備ができました。

次のステップ

具体的な方法は以下の中から自分に合ったものを選んでください。

計算よりも、地球や地球の影や、月を縮尺して 作図する事で月の大きさと月までの距離を求める。

コースA

簡単な比例計算で月の直径をまず求める 方法。方法の理解はやや直感を必要とします。

コースB

数式を使う事に抵抗がない人は、原理どおりに式をたて 方程式にして解けば簡単に求められます。

コースC

月食を楽しもう ページ一覧

「月食を楽しもう」は2000年6月に公開された記事を編集・再構成したものです